Pythagorean theorem calculator for accurate & timely computing
Our free tool enables you to determine the unknown side of a Pythagorean equation in a blink of an eye. Pythagorean theorem calculations have never been easier!
Pythagorean theorem calculator
Please provide any 2 values below to solve the Pythagorean equation: a2 + b2 = c2.
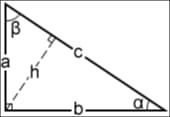
What there is to know about the Pythagoras theorem calculator
Our calculator helps determine the geometrical expression of the Pythagorean equation with little effort or time input from you. With our seamless interface and a wide variety of features, you can make your calculations as easy as pie.
This calculating tool is based on Pythagoras' theorem, which explains the fundamental relation between the three sides of a right triangle.
What is the Pythagorean theorem?
The Pythagorean theorem depicts the fundamental concept of Euclidean geometry, outlining the relationship between the three sides of a right-angled triangle. According to this theorem, the sum of the legs' squares in a triangle is equal to the square of the hypotenuse (the longest side of a triangle). It can also be reflected in this formula:
a2 + b2 = c2, where a and b refer to the legs of a triangle and c – the hypotenuse.
Named after the ancient Greek philosopher Pythagoras, this theorem describes the cardinal principle of geometry. Although there is no solid proof, Pythagoras is said to be the first one to prove it.
Pythagorean theorem formula
The Pythagorean theorem enables you to discover the length of the third side of a right-angled triangle, given that you know the length of two other sides. It can also be depicted in this formula:
a2 + b2 = c2, where a and b refer to the triangle legs, and c is the hypotenuse.
What is the Pythagorean theorem calculator?
A Pythagorean calculator is a smart tool that allows you to determine any side of a right triangle easily and momentarily. All you need is a few minutes of your time and the lengths of the other two sides of the triangle. Just fill out the input tabs and click "Calculate" to get precise results.
Frequently Asked Questions
You don't need specific technical knowledge to use our calculator. Discover our straightforward interface and seamless design, and calculate the Pythagorean theorem in just a few clicks:
- Choose the side of the right triangle you want to calculate.
- Write the values for the other two sides.
- Tap the "Calculate" button to get the results.
- Click "Reset" to clear tabs.
A set of three positive numbers for a and b sides and the hypotenuse c that agree with Pythagoras theorem is called a Pythagorean triple. 3, 4, and 5 are the lowest possible values for it.
Considering the a2 + b2 = c2 formula, let's view an example of a Pythagorean triple:
32 + 42 = 52
9+26=25
25=25
As evident from its name, the hypotenuse formula solves the Pythagorean theorem for the hypotenuse, c. It is a version of a theorem formula that allows one to determine the length of a hypotenuse. You can do so by taking the square root of both sides of a right-angled triangle. So, from the equation a2 + b 2 = c2, we extract the hypotenuse formula c = √ (a2 + b2).
To grasp a better understanding of Pythagoras' theorem, let's take a look at these examples.
- In a right triangle ABC, the base BC is 12 units, height AB – 5 units. To find the length of AC, we use the Pythagorean equation:
AB2 + BC2 = AC2
AC2 = 52 + 122
AC = (52 + 122 )½ ; = √ (52 + 122)
AC = 13.
2. Find the value of the QR side in a right-angled triangle PQR with angle Q = 90°;, PQ = 8 units, PR = 10 units.
PR2 = PQ
2 + QR2
102 = 82+ QR
2
QR2 = 102 - 82
QR =(10
2 - 82)½; = √(102 + 8
2)
QR = 6.

